Tensors have the following general properties:
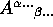and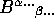 
are M/N tensors, so are 
,
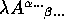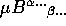and
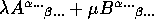for any 
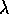and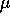 
. Thus tensors of a given type form
a vector space 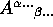. is a M/N tensor and
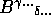is of type M'/N', then the outer product
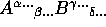is a tensor
of type M+M'/N+N'.
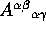is constructed from
[ 
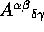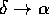or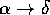 
]. Note however that there may be several ways of
contracting and they give different tensors.
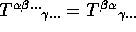and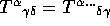 
, or anti- symmetric . However symmetric or anti- symmetric pairs of
indices with one index up and the other down cannot be defined since the
relationship need not hold in all frames.